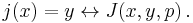Kunen's inconsistency theorem
In set theory, a branch of mathematics, Kunen's inconsistency theorem, proved by Kenneth Kunen (1971), shows that several plausible large cardinal axioms are inconsistent with the axiom of choice.
Some consequences of Kunen's theorem are:
- There is no non-trivial elementary embedding of the universe V into itself. In other words, there is no Reinhardt cardinal.
- If j is an elementary embedding of the universe V into an inner model M, and λ is the smallest fixed point of j above the critical point κ of j, then M does not contain the set j "λ (the image of j restricted to λ).
- There is no ω-huge cardinal.
- There is no non-trivial elementary embedding of Vλ+2 into itself.
It is not known if Kunen's theorem still holds in ZF (ZFC without the axiom of choice), though Suzuki (1999) showed that there is no definable elementary embedding from V into V.
Notice that Kunen used Morse–Kelley set theory in his proof, if the proof is re-written to use ZFC, then one must add the assumption that j is a definable class function, i.e. that there is a formula J in the language of set theory such that for some parameter p∈V for all sets x∈V and y∈V:
Otherwise one could not even show that j "λ exists as a set. The forbidden set j "λ is crucial to the proof. The proof first shows that it cannot be in M. The other parts of the theorem are derived from that.
See also
References
- Kanamori, Akihiro (2003), The Higher Infinite : Large Cardinals in Set Theory from Their Beginnings (2nd ed.), Berlin, New York: Springer-Verlag, doi:10.1007/978-3-540-88867-3, ISBN 978-3-540-00384-7
- Kunen, Kenneth (1971), "Elementary embeddings and infinitary combinatorics", J. Symbolic Logic 36 (3): 407–413, doi:10.2307/2269948, JSTOR 2269948, MR0311478
- Suzuki, Akira (1999), "No elementary embedding from V into V is definable from parameters", The Journal of Symbolic Logic 64 (4): 1591–1594, doi:10.2307/2586799, ISSN 0022-4812, MR1780073
- Zapletal, Jindřich (1996), "A new proof of Kunen's inconsistency", Proceedings of the American Mathematical Society 124 (7): 2203–2204, doi:10.1090/S0002-9939-96-03281-9, ISSN 0002-9939, MR1317054